Dtyjlui

自転車のクランクにおける疲労破壊の例。

疲労（ひろう、Fatigue）は、物体が力学的応力を継続的に、あるいは繰り返し受けた場合にその物体の機械材料としての強度が低下する現象。金属で発生するものは金属疲労(Metal fatigue)として一般に知られているが、金属だけではなく樹脂やガラス、セラミックスでも起こり得る。また、力学的応力だけではなく電圧や温度の継続的または繰り返し負荷によって絶縁耐力や耐熱性が低下する現象を指すこともあるが一般的ではない。こちらはむしろ経年劣化と呼ぶ。

現象および機構

物体はその機械的強度；引張強度(UTS,降伏応力)より小さい力学的応力を一時的に受けても破壊されることはなく、弾性範囲内であれば応力を取り除くことにより元の状態に復元する。しかしながら、巨視的には弾性範囲内の小さい応力であっても、原子論レベルの微視的状態においては、ごく一部の原子がもとあった場所に戻らない非弾性的振る舞いを起こし(転位現象)、それが蓄積されることによって強度が劣化する。繰り返し応力を受ける場合、破壊された断面を観察すると縞状の模様が観察されることが面心立方金属（Al、Cu、オーステナイト鋼）に多く見られ、その襞の1つが一振幅の負荷に相当しストライエーション（Striation）や固執すべり帯(Persistent slip bands;PSBs)と呼ばれる。

疲労による機械的強度の低下は多くの場合、始めに物体に微小な割れ目（クラック）が発生し、繰り返し応力を受けることによって割れ目が次第に大きくなる機構による。物体に応力が加えられると弾性範囲内であっても拡散現象などによってわずかな物質の移動が発生して応力を緩和しようとする。物質の移動によって微小な割れ目が発生すると、その割れ目の先端において応力が大きくなり、割れ目が進行するようになる。物体を構成する物質の一部が、応力を受けて弾性率や強度の小さい別の物質に変化する場合にも同様の現象が起こる。

疲労破壊は温度、表面処理、金属的微細組織、酸化・不活性気体、残留応力、物体間の接触(フレッティング)など様々な環境要因に影響される。

疲労応力

繰返し応力波形(正弦波)

変動応力波形(ランダム応力)

材料に負荷する応力が一定ではなく、時間に対して変動することによって引き起こされる破壊が疲労の定義の1つである^{[注釈 1]}。そのような疲労応力を発生させる荷重を疲労荷重(fatigue loading)または動荷重(dynamic loading)と呼ぶ。外的な荷重が負荷しなくても、このような繰り返しの疲労応力は発生し得るので注意が必要である。例えば、部材に温度変化が発生する場合は熱応力による疲労破壊が発生する可能性がある。

繰返し応力

疲労を引き起こす応力の中で、応力振幅、平均応力が一定の周期的な応力を繰返し応力(repeated stress)、繰返し応力を引き起こす荷重を繰返し荷重と呼ぶ^[1]。疲労の試験では実現の容易さのため、繰返し応力を正弦波の応力波形を与えて材料の疲労特性を試験することが多い。このような繰り返し応力を受ける実際の機械構造物としては、一定荷重を支えて走行する車軸などがある。以下に繰返し応力の重要因子を示す。

σ_max:最大応力

σ_min:最少応力

Δσ:応力範囲(=σ_max - σ_min)

σ_a:応力振幅(=Δσ/2)

σ_m:平均応力(=(σ_max + σ_min)/2)

R:応力比(=σ_min / σ_max)

N:繰り返し数

f:周波数

特に、R = -1のときを両振り応力、R = 0のときを片振り引張応力、R = －∞のときを片振り圧縮応力と呼ぶ。

変動応力

応力振幅、平均応力が不規則に時間的に変化するような応力を変動応力(fluctuating stress)、変動応力を引き起こす荷重を変動荷重と呼ぶ^[2]。特に、実際に構造物が受ける応力を実働応力(service stress)と呼び^[3]、この応力を精度良く知ることが疲労対策の重要点である。実働応力は、実際に運用中の構造部材にひずみゲージを用いて直接測定したり、加速度などから間接的に測定する^[4]。実働応力は周期的な応力になるとは限らず、不規則な波形のランダム応力になることも多い^[3]。

S-N曲線

詳細は「S-N曲線」を参照

アルミニウムのS-N曲線

材料がどれくらいの繰り返し応力に耐えられるか、どれくらいの回数を与えるとどれくらいの応力で破断するのかをあらわすためにはS-N曲線（S-N curve）が広く使われている。S-N曲線は、縦軸に応力振幅（stress amplitude）あるいは応力範囲(stress range)、横軸にその応力を繰り返し負荷して破断するまでの繰り返し回数（number of cycles）の対数で表されるグラフである。S-N曲線は、世界で最初にS-N曲線を見つけ出したドイツの技術者アウグスト・ヴェーラーの名前から、ヴェーラー曲線（Wöhler curve）」と呼ばれることもある。材料のS-N曲線を求めるためには、疲労試験装置に試験片を取り付け、破断するまで繰り返し応力を加えて求められる。

繰り返し数が10⁵回程度以上で発生する疲労破壊を高サイクル疲労(high cycle fatigue)と呼び、10⁴回程度以下で発生するものを低サイクル疲労(low cycle fatigue)あるいは塑性疲労と呼ぶ^[5]^[6]。低サイクル疲労では負荷される応力が材料の降伏応力以上となるため、材料の疲労試験をする際には、繰り返し応力振幅を一定にして試験する場合と繰り返しひずみを一定にして試験する場合で結果が異なる。繰り返しひずみ一定の場合の疲労評価を表す場合は、応力振幅の代わりに全塑性ひずみ幅Δε_tを用いたε-N曲線が使用される^[7]。またさらに、10⁷回以上の繰り返し数でも疲労破壊が起こる場合があり、このような繰り返し数領域での疲労を超高サイクル疲労(very high cycle fatigue)あるいはギガサイクル疲労(Gigacycle fatigue)などと呼ぶ^[8]。

S-N曲線であらわされる耐久性は、装置上で試験片に、ごく単純な正弦波状の繰り返し応力を加え続けたものであり、材料の形状や温度変化、腐食など性質の変化、時間的に非連続的な応力がかかることなどは考慮されていない。そのため実際に材料が使われている状況とは違うことを考慮することが必要である^[9]。

破断する確率を統計的(Stochastic)に取り扱う場合にはワイブル分布が用いられる。

疲労限度

詳細は「疲労限度」を参照

鉄鋼系材料であれば、10⁶ - 10⁷回ほど繰り返したところで、S-N曲線がほぼ横ばいになり、それ以下の応力では何度回数を繰り返しても破断しないと考えられる応力振幅の限界点が存在する場合がある。この時の応力振幅を疲労限度(Fatigue limit)または耐久限度(endurance limit)と呼び、長期間変動荷重に晒されるものを設計する際の目安になる。ただし、対象となる部材の表面状態や欠陥・切欠き等の有無、雰囲気、外気温度、繰り返し応力の加わり方などによって疲労限度は大きく異なり、あるいは疲労限度が存在しなくなる場合も存在する。疲労の許容応力をどのように評価するかは、実験値の疲労限度のみならず、対象物の実際の使用状況を検討し、多くの影響因子を考慮して決める必要がある。また、右下がりに傾斜している範囲の応力を時間強度(strength at finite life)あるいは単に疲労強度(fatigue strength)と呼び^{[注釈 2]}、例えば10⁶回に対応する時間強度(応力)を10⁶時間強度などと呼ぶ。アルミニウムや黄銅、あるいはプラスチックなどは、鉄鋼系材料のような明確な疲労限度を持たず、繰り返し回数を多くするほど破断応力は低下する傾向を示す。このような材料では10⁷ - 10⁸回程度の時間強度を疲労限度と同じような目安と見なして取り扱う^[10]。

寿命予測式

材料が疲労によって破断するまでの応力繰り返し数(ASTMにおける「疲労寿命」)を予測する代表的な方法について以下に示す。

バスキン則とコフィン-マンソン則

高サイクル疲労のような低ひずみ疲労には、次のバスキン則(Basquin rule)がある^[11]。

Delta epsilon _{e}N^{a}=C_{e}

… (1)

あるいは

Delta sigma N^{a}=EC_{e}

… (2)

ここで

Δε_e: 弾性ひずみ範囲

Δσ: 応力範囲

E: 弾性率

N: 破断に至るまでの繰り返し数

a: 疲労強度指数(おおむね0.07から0.12の間の材料定数)

C_e: 疲労強度係数(材料定数)

一方、低サイクル疲労のような高ひずみ疲労には次のコフィン-マンソン則(Coffin-Manson rule)がある^[11]。

Delta epsilon _{p}N^{b}=C_{p}

… (3)

Δε_p: 塑性ひずみ範囲

b: 疲労延性指数(おおむね0.5から0.7の間の材料定数)

C_p: 疲労延性係数(材料定数)

バスキン則もコフィン-マンソン則も、応力振幅一定あるいはひずみ振幅一定の前提下での破断に至るまでの繰り返し数を予測するもので、S-N曲線あるいはε-N曲線を近似的に予測する式となる。

マイナー則

変動応力を受ける場合の寿命予測には、マイナー則または線形累積損傷則と呼ばれる経験則が使用される。

詳細は「線形累積損傷則」を参照

線形累積損傷則により寿命を予測するには、実働応力の応力頻度分布を求める必要がある。このために種々の応力頻度計数法が提案されており、遠藤らにより提案されたレインフロー法が良く使用されている^[12]^[13]。

予防策、疲労設計

材料力学を用いてあらかじめ余裕を持った設計にすることで疲労による破壊をある程度防ぐことができるが、用途によっては重量やコスト、安全性などの制約から十分な余裕を持てない場合もある（例えば航空機、原子炉など）。このような場合には、繰り返し荷重がかかる構造物の運用中に検出できない初期欠陥からき裂が発生・進展することを前提として寿命を評価する損傷許容設計が採用され^[14]、応力を受ける部材を定期的に交換するか、あるいは定期的な検査において部材の微小な割れ目を検出して破壊に至る前に使用を中止し、新しい部材に交換する手法を用いる。割れ目の検出は超音波探傷検査や浸透探傷検査、X線写真などの非破壊検査を用い、検出限界と設計の余裕から検査の頻度を規定することができる。但し、疲労は状況によって進行速度の変動する幅が大きいため、事前の試験方法を誤ったり、使用基準を守らなかったり、修理や改造などによって初期の設計から外れたりすると、予想より早く破断に至り事故につながることがある。

歴史

材料の疲労現象は古くから経験的に知られていたと考えられるが、18世紀の産業革命による機械工業の発達以降、疲労による破壊事故が大きく社会的に問題として認識されるようになった^[15]。産業革命により、それまでの水や馬といった小さな力の動力源から蒸気機関という大きな力の動力源を使用するようになったためと考えられる^[16]。対策のため、各国で学者や技術者による委員会が組織され、疲労の研究が本格的に進められるようになった^[15]。

材料に対する「疲労」という用語を最初に用いたのはフランスのジャン＝ヴィクトル・ポンスレ(Jean-Victor Poncelet)である^[17]。ポンスレは1825年頃からメスの兵学校で、材料の疲労についての講義をしていたといわれる^[17]。ポンスレによる疲労の発生機構の仮説は、繰返し荷重によって鉄の繊維状組織が結晶化して脆化することによる、というものであった^[18]。

疲労の本質に迫った実験としては、1837年にドイツのウィルヘルム・アルバート(Wilhelm Albert)が、鉱山の鉄製チェーンの疲労に関する実験結果を報告したものが最初である^[19]^[20]。アルバートは鉱山の巻き上げ機の鉄製の鎖が時折突然破断することを経験して、その原因を調査する中で、巻き付けの繰返しが原因と推測して鎖用の疲労試験を考案、実施した^[16]。試験では、安定した繰返し荷重を実験対象のチェーンに与えるために、水車の仕組みを利用していた^[19]。この試験により、アルバートは、静的な破断限界より小さな力でも繰り返し作用することで突然破断することを見出した^[16]。

1853年にはフランスのモラン(A. Morin)が郵便馬車の車軸について、走行距離が7万キロメートルを越えると破壊が始まることから、この距離を走行した時点で点検・交換することを指示した記録が残されている^[17]。これが疲労破壊に対する予防保全の最初の例である。

1856年から1869年にかけて、ドイツの技術者であったアウグスト・ヴェーラー（August Wöhler）は、自ら回転曲げ疲労試験機を作り出し、鉄道用車軸を使って疲労実験を繰り返し、疲労を科学的に分析した^[21]。その結果、S-N曲線により疲労破壊特性を整理可能なことを発見した^[21]。1870年、ヴェーラーは、車輪に10⁶回程度振動を繰り返した後は、どれだけ回数を繰り返しても耐久応力が下がらず、永久に耐え続けられるある一定の応力があることを発表した。このことをヴェーラー自身は耐久限度（Endurance limit）と呼んでいたが、後に疲労限度と呼ばれるものと全く同じである。

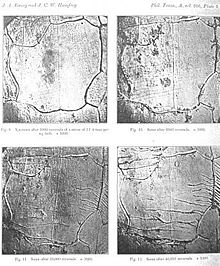
疲労亀裂の顕微鏡写真Micrographs showing how surface fatigue cracks grow as material is further cycled. From Ewing & Humfrey, 1903

1963年、ポール・パリス(Paul Paris)らにより、き裂の繰返し荷重1サイクル当たりの進展速度(da/dN)が応力拡大係数で整理でき、進展速度を予測可能であることが発表された^[22]。1971年、ウォルフ・エルバー(Wolf Elber)により、き裂先端部の局所的塑性変形により引張荷重下でもき裂が閉じるき裂閉口現象の発生機構とその重要性について発表された^[23]。

疲労が関与した大事故

疲労が原因として関与した事故の内、特に歴史的に有名な例を示す。

1842年：ヴェルサイユ列車事故（車軸の破損）

1954年：コメット連続墜落事故

機体設計時に疲労試験を行っていたが、強度試験をした機体で疲労試験も行ってしまったため応力集中部が塑性硬化を起こし、疲労強度が大きくなり、実際の使用条件に対して寿命を1桁大きく見積もってしまった。

1980年：北海油田の石油プラットフォーム「アレクサンダーキーランド」の転覆事故（構造体溶接部の破損）

溶接部の疲労試験も点検も行っていなかった。

「アレクサンダーキーランド」の艤装構造と破壊箇所

1985年：日本航空123便墜落事故

日本航空によって運行されていたボーイング747SR型機が墜落し、死者520名を出し、過去最悪の航空機事故となった^[24]。直接の原因は圧力隔壁の疲労破壊で、同箇所の事故以前に行われたボーイング社の修理が適切ではなかったため疲労破壊発生に至った^[24]。

1989年：ユナイテッド航空232便不時着事故（エンジンファンの破損）

部品を製造した直後から割れが進行していたにもかかわらず検査によって検出できなかった。

1992年：エル・アル航空1862便墜落事故（エンジン接続ピンの破損）

1994年：韓国聖水大橋崩落事故（鋼材接続ピンおよび溶接部の破損）

検査によって溶接不良を確認していたにもかかわらず放置され、交通量の増大によって急激に疲労が進んでしまった。

1998年：エシェデ鉄道事故

ドイツ高速列車ICEが時速200キロメートルで走行中に脱線し、101名の死者を出した事故となった^[25]。原因は弾性車輪の外輪と呼ばれる鉄製タイヤ部分の疲労破壊によるものであった^[25]。

2002年：チャイナエアライン611便空中分解事故（機体スキンの破損）

2007年：エキスポランド　ジェットコースター横転事故（車軸の破損）

脚注

注釈

^ 一定応力下で時間が経過し、破断に至る現象はクリープと呼ばれる。

^ ただし疲労限度も含めたその材料の一般的な疲労に対する強度のことを疲労強度と呼ぶことも多い。

出典

^ 機械工学辞典 p.345

^ 機械工学辞典 p.1211

^ ^a^b機械工学辞典 p.533

^ 疲労設計便覧 p.205

^ 機械工学辞典 p.1109

^ 疲労設計便覧 p.8

^ 疲労設計便覧 p.133

^ 塩澤和章「高強度鋼の超高サイクル疲労に関する研究動向 (PDF) 」、『NACHI TECHNICAL REPORT』第14巻、不二越、2007年10月、 1頁。

^ 金属疲労の盲点

^ 機械工学辞典 p.1110

^ ^a^b疲労設計便覧 pp.129–130

^ 疲労き裂 p.182

^ 遠藤達雄・松石正典・光永公一・小林角市、1974、「「Rain Flow Method」の提案とその応用 (PDF) 」、『九州工業大学研究報告』、九州工業大学

^ 疲労設計便覧 p.2

^ ^a^b金属疲労のおはなし pp.18–19

^ ^a^b^c境田ほか 2011, p. 76.

^ ^a^b^c絵とき「金属疲労」基礎のきそ pp.82–83

^ 機械材料学 p.37

^ ^a^b図解入門よくわかる最新金属疲労の基本と仕組み pp.12–14

^ 境田ほか 2011, p. 77.

^ ^a^b絵とき「金属疲労」基礎のきそ pp.42–43

^ Paul C. Paris; Mario P. Gomez; William E. Anderson (1961年1月). “A Rational Analytic Theory of Fatigue”. The Trend in Engineering 13: 9-14.

^ 疲労き裂 p.4

^ ^a^b境田ほか 2011, p. 79.

^ ^a^b境田ほか 2011, p. 80.

参考文献

日本機械学会（編）、2007、『機械工学辞典』第2版、丸善 ISBN 978-4-88898-083-8

日本材料学会（編）、2008、『疲労設計便覧』第3版、養賢堂 ISBN 978-4-8425-9501-9{{ISBN2}}のパラメータエラー: 無効なISBNです。

佐藤建吉、2008、『絵とき「金属疲労」基礎のきそ』、日刊工業新聞社 ISBN 978-4526061035

曽山義朗・渡部正気・古市博、1998、『金属疲労の盲点』、株式会社アイピーシー

城野政弘・宋智浩、2005、『疲労き裂　き裂開閉口と進展速度推定法』初版、大阪大学出版会

平川賢爾・大谷泰夫・遠藤正浩・坂本東男、2004、『機械材料学』第1版、朝倉書店〈基礎機械工学シリーズ 2〉 ISBN 978-4-254-23702-3

酒井達雄、2011、『図解入門よくわかる最新金属疲労の基本と仕組み』第1版、秀和システム ISBN 978-4-7980-2972-6

西島敏、2007、『金属疲労のおはなし』第1版第1刷、日本規格協会〈おはなし科学・技術シリーズ〉 ISBN 978-4-542-90283-1

境田彰芳・上野明・磯西和夫・西野精一・堀川教世、2011、『材料強度学』第1版、コロナ社〈機械系　教科書シリーズ〉 ISBN 978-4-339-04476-8

外部リンク

金属材料の疲労破壊デジタルアーカイブ - 物質・材料研究機構

[1] 一定応力下で時間が経過し、破断に至る現象はクリープと呼ばれる。

[11] ただし疲労限度も含めたその材料の一般的な疲労に対する強度のことを疲労強度と呼ぶことも多い。

[機械工学辞典_345-2] 機械工学辞典 p.345

[機械工学辞典_1211-3] 機械工学辞典 p.1211

[機械工学辞典_533-4] 機械工学辞典 p.533

[疲労設計便覧_205-5] 疲労設計便覧 p.205

[機械工学辞典_1109-6] 機械工学辞典 p.1109

[疲労設計便覧_8-7] 疲労設計便覧 p.8

[疲労設計便覧_133-8] 疲労設計便覧 p.133

[9] 塩澤和章「高強度鋼の超高サイクル疲労に関する研究動向 (PDF) 」、『NACHI TECHNICAL REPORT』第14巻、不二越、2007年10月、 1頁。

[金属疲労の盲点-10] 金属疲労の盲点

[機械工学辞典_1110-12] 機械工学辞典 p.1110

[疲労設計便覧_129-130-13] 疲労設計便覧 pp.129–130

[疲労き裂_182-14] 疲労き裂 p.182

[15] 遠藤達雄・松石正典・光永公一・小林角市、1974、「「Rain Flow Method」の提案とその応用 (PDF) 」、『九州工業大学研究報告』、九州工業大学

[疲労設計便覧_2-16] 疲労設計便覧 p.2

[金属疲労のおはなし_18-19-17] 金属疲労のおはなし pp.18–19

[FOOTNOTE境田ほか201176-18] 境田ほか 2011, p. 76.

[絵とき「金属疲労」基礎のきそ_82-83-19] 絵とき「金属疲労」基礎のきそ pp.82–83

[機械材料学_37-20] 機械材料学 p.37

[図解入門よくわかる最新金属疲労の基本と仕組み_12-14-21] 図解入門よくわかる最新金属疲労の基本と仕組み pp.12–14

[FOOTNOTE境田ほか201177-22] 境田ほか 2011, p. 77.

[絵とき「金属疲労」基礎のきそ_42-43-23] 絵とき「金属疲労」基礎のきそ pp.42–43

[24] Paul C. Paris; Mario P. Gomez; William E. Anderson (1961年1月). “A Rational Analytic Theory of Fatigue”. The Trend in Engineering 13: 9-14.

[疲労き裂_4-25] 疲労き裂 p.4

[FOOTNOTE境田ほか201179-26] 境田ほか 2011, p. 79.

[FOOTNOTE境田ほか201180-27] 境田ほか 2011, p. 80.

搜尋此網誌