四面体形分子構造
| 四面体形分子構造 | |
|---|---|
 | |
| 例 | CH4、PO3− 4、SO2− 4 |
| 点群 | Td |
| 立体数 | 4 |
| 配位数 | 4 |
| 結合角 | ≈109.5° |
化学において、四面体形分子構造(しめんたいがたぶんしこうぞう、Tetrahedral molecular geometry)とは、中心原子に配位する4個の置換基が四面体の頂点に位置した分子の幾何配置のことである。メタン[1][2]やその他の第14族元素水素化物のように、4個の置換基がすべて同じときその結合角はcos−1(−1/3) = 109.4712206...° ≈ 109.5°である。この完全に対称な四面体は点群Tdに属するが、ほとんどの四面体分子はそれほど対称性は高くない。四面体分子はキラルになることができる。
目次
1 四面体形分子の例
1.1 主族元素
1.2 遷移金属
1.3 水の構造
2 二重四面体形構造
3 例外と歪み
3.1 四面体の反転
3.2 平坦化
3.3 中心原子を持たない四面体形分子
4 脚注
5 関連項目
6 外部リンク
四面体形分子の例
主族元素

三フッ化チアジル
実質的に飽和した有機化合物および、ケイ素、ゲルマニウム、スズの化合物は四面体形である。しばしば四面体形分子は、四酸化キセノンや過塩素酸イオン、硫酸イオン、リン酸イオンのように配位子と複数の結合をする。三フッ化チアジルではS-N間の結合が三重結合である[3]。
アンモニアは、その非共有電子対を配位子の一つと見なすと四面体形に分類することができるが、非共有電子対の影響のため、そのH-N-H角は109.4°より小さい107°である。
遷移金属
四面体形分子構造はd0またはd10配置を持つ金属錯体まで広範囲にわたる。四面体形構造を持つ金属化合物には、テトラキス(トリフェニルホスフィン)パラジウム(0)、ニッケルカルボニル、塩化チタン(IV)などがある。鉄(II)、コバルト(II)そしてニッケル(II)などd軌道が満たされていない錯体もしばしば四面体形である。
水の構造
気相において、単一の水分子は2つの水素原子と2つの孤立電子対によって囲まれた酸素原子を持ち、H2O幾何配置は非結合性の孤立電子対を考慮することなく折れ線形と単純に記述される。
しかしながら、液体の水あるいは氷では、これらの孤立電子対は近傍の水分子と水素結合を形成する。酸素原子の周りの水素原子の最も一般的な配置は、2つの水素原子が酸素原子と共有結合し、2つが水素結合によって付いた四面体形である。水素結合の距離は変化するため、これらの水分子の多くは対称的ではなく、4つの結び付いた水素結合間で一時的な非正四面体を形成する[4]。
二重四面体形構造
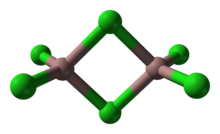
Al2Br6(三臭化アルミニウム)およびGa2Cl6(三塩化ガリウム)がとる二重四面体構造
多くの化合物および錯体が二重四面体形構造をとる。このモチーフでは、2つの四面体が一つの縁を共有している。無機ポリマーである硫化ケイ素は縁を共有した四面体の無限鎖を特徴とする。
例外と歪み

アンモニアの反転
主族元素や有機化学では四面体の反転がよく起こる。いわゆるワルデン反転では、炭素の立体化学が反転する。また、アンモニアは平面形を経由して窒素反転を起こす。
四面体の反転
分子の幾何学的制約によって四面体が大きく歪められることがある。“反転する炭素”を特徴とする化合物の炭素は三角錐形である[5]。
平坦化
四面体形は結合角が増加することによっても歪められ、極端なケースでは平坦化する。このような現象はフェネストランと呼ばれる化合物でみられる。
中心原子を持たない四面体形分子
いつすかの分子は中心原子を持たない四面体形幾何配置を持つ。無機化合物での一つの例は四リン(P4)である。P4は四面体の頂点に4つのリン原子を持ち、それぞれが残りの3つのリン原子と結合している。有機化合物での一つの例はテトラヘドラン(C4H4)である。テトラヘドランは4つの炭素原子を持ち、それぞれの炭素原子が1つの水素原子と残り3つの炭素原子を結合している。
脚注
^ Alger, Nick. “Angle Between 2 Legs of a Tetrahedron”. Maze5.net. 2017年6月28日閲覧。
^ Brittin, W. E. (1945). “Valence Angle of the Tetrahedral Carbon Atom”. J. Chem. Educ. 22 (3): 145. doi:10.1021/ed022p145.
^ G. L. Miessler and D. A. Tarr “Inorganic Chemistry” 3rd Ed, Pearson/Prentice Hall publisher, ISBN 0-13-035471-6.
^ Mason, P. E.; Brady, J. W. (2007). “"Tetrahedrality" and the Relationship between Collective Structure and Radial Distribution Functions in Liquid Water”. J. Phys. Chem. B 111 (20): 5669–5679. doi:10.1021/jp068581n.
^ Inverted geometries at carbon Kenneth B. Wiberg Acc. Chem. Res.; 1984; 17(11) pp 379 - 386; doi:10.1021/ar00107a001
関連項目
- VSEPR理論
- 混成軌道
- 分子構造
外部リンク
- Examples of Tetrahedral molecules
- Animated Tetrahedral Visual
- Elmhurst College
- Point group Symmetries
3D Chem - Chemistry, Structures, and 3D Molecules
IUMSC - Indiana University Molecular Structure Center]- Molecular Modeling
| ||||||||||||||||||
