ライフゲーム
この記事には参考文献や外部リンクの一覧が含まれていますが、脚注による参照が不十分であるため、情報源が依然不明確です。適切な位置に脚注を追加して、記事の信頼性向上にご協力ください。(2018年8月) |
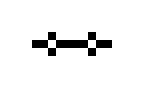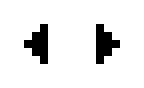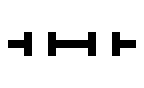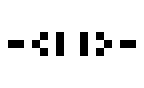
ペンタデカスロンと呼ばれるパターン
ライフゲーム (Conway's Game of Life[1]) は1970年にイギリスの数学者ジョン・ホートン・コンウェイ (John Horton Conway) が考案した生命の誕生、進化、淘汰などのプロセスを簡易的なモデルで再現したシミュレーションゲームである。単純なルールでその模様の変化を楽しめるため、パズルの要素を持っている。
生物集団においては、過疎でも過密でも個体の生存に適さないという個体群生態学的な側面を背景に持つ。セル・オートマトンのもっともよく知られた例でもある。
目次
1 概要
2 ライフゲームのルール
3 パターンの例
3.1 固定物体の例
3.2 振動子の例
3.3 移動物体の例
3.4 繁殖型の例
3.5 長寿型の例
4 バリエーション
5 ライフゲームを用いた計算機
6 脚注
7 参考文献
8 関連項目
9 外部リンク
概要
我々が暮らす空間、さらには時間が連続的なものであるか、それとも非連続的なものであるのか、という問いはギリシア時代から思索の対象となってきた。セル・オートマトンはその問いに答えるものではないが、空間、時間が不連続であった場合、どのような世界が形成されるのかを示してくれる。
セル・オートマトンは、四角形などのセルによって分割された空間において、時間に最小単位が存在する場合の計算モデルである。1940年代にジョン・フォン・ノイマンとスタニスワフ・ウラムによって考案された。当時はコンピュータが発明された直後であり、セル・オートマトンの研究は、方眼紙と筆記具によるものである。フォン・ノイマンの関心は自己複製機械にあり、2次元セル・オートマトンによる自己複製機械の例を1952年に示している。
セル・オートマトンが研究者以外の興味をひくきっかけとなったのが、ライフゲームである。1970年10月の『サイエンティフィック・アメリカン』誌のマーチン・ガードナーのコラム上で紹介されたところ多くの反響を呼んだ。サイエンティフィック・アメリカン誌が読者からの手紙を中心とした記事を何度も組んだほどである。興味深いことにライフゲームはチューリング完全(万能チューリングマシンの働きをするパターンが構成可能)であることが証明されている。これは、ライフゲームで、計算機で実行可能な全ての計算について、対応するパターンを作ることができるということを表している。
ライフゲームの考案後すぐに、移動物体であるグライダーパターンと、長寿型のR-ペントミノパターンが発見された。当時は、このようなゲームの研究を目的として、コンピュータを利用できたのは限られた人々であったが、それらの人々の間にライフゲームは流行した。夜間あるいは未使用のコンピュータ上でライフゲームのプログラムが動かされることとなり、興味深いパターンが多数発見された。後にマイクロコンピュータの普及により、一定の人気を持つアプリケーションとして現在に至っている。
その後、セル・オートマトンの研究はライフゲームのような2次元のタイプではなく、1次元を中心に進んだ。1980年には、スティーブン・ウルフラムによって1次元セル・オートマトンの4分類が完成し、クリストファー・ラングトンによって「カオスの縁」と呼ばれる概念が確立した。3次元以上のセル・オートマトンも研究対象となっている。
ライフゲームのルール
ライフゲームでは初期状態のみでその後の状態が決定される。碁盤のような格子があり、一つの格子はセル(細胞)と呼ばれる。各セルには8つの近傍のセルがある (ムーア近傍) 。各セルには「生」と「死」の2つの状態があり、あるセルの次のステップ(世代)の状態は周囲の8つのセルの今の世代における状態により決定される。
セルの生死は次のルールに従う。
- 誕生
- 死んでいるセルに隣接する生きたセルがちょうど3つあれば、次の世代が誕生する。
- 生存
- 生きているセルに隣接する生きたセルが2つか3つならば、次の世代でも生存する。
- 過疎
- 生きているセルに隣接する生きたセルが1つ以下ならば、過疎により死滅する。
- 過密
- 生きているセルに隣接する生きたセルが4つ以上ならば、過密により死滅する。
下に中央のセルにおける次のステップでの生死の例を示す。生きているセルは■、死んでいるセルは□で表す。
| 誕生 | 生存(維持) | 死(過疎) | 死(過密) |
|---|---|---|---|
 |  |  |  |
パターンの例
ライフゲームでは世代を経ることで最終的に死滅する図形もある。
生き延びる場合の変化は4パターンに分類することができる。
固定物体は世代が進んでも同じ場所で形が変わらないものを指す。
振動子はある周期で同じ図形に戻るものを指す。
移動物体は一定のパターンを繰り返しながら移動していくものを指す。
繁殖型はマス目が無限であれば無限に増え続けるパターンである。
コンウェイは「生きたセルの数が無限に増えつづけるパターンはありうるか」という問題に50ドルの懸賞金をかけた。コンウェイ自身は、そのようなパターンとして「周期的だが次々にグライダーを打ち出すもの」や「移動しながら通過した後に破片を残すもの」の存在を予想し、前者を「グライダー銃」、後者を「シュシュポッポ列車」と呼んだ。1970年11月、ビル・ゴスパーらは、初めてグライダー銃の具体例を挙げて賞金を獲得した。後にシュシュポッポ列車の具体例も与えられている。繁殖型としては、移動しながらグライダーを打ち出す「宇宙の熊手」(space rake) と呼ばれるものや、四方に向かって成長する「マックス」と呼ばれるものなど、様々なパターンが見付かっている。
4つの分類における単純な例を以下に示す。
固定物体の例
| ブロック | 蜂の巣 | ボート | 船 | 池 |
|---|---|---|---|---|
 | 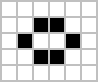 |  |  |  |
振動子の例
周期が2で発生しやすい振動子には以下のようなものがある。
| ブリンカー | ヒキガエル | ビーコン | 時計 |
|---|---|---|---|
ちなみに周期が3以上のものでは、以下のようなものがある。
| パルサー | 八角形 | 銀河 | ペンタデカスロン |
|---|---|---|---|
 |  |  |  |
移動物体の例
| グライダー | 軽量級宇宙船 | 中量級宇宙船 | 重量級宇宙船 |
|---|---|---|---|
 | □□□■□□ □■□□□■ ■□□□□□ ■□□□□■ ■■■■■□
| □□□■■□□ □■□□□□■ ■□□□□□□ ■□□□□□■ ■■■■■■□
|
繁殖型の例
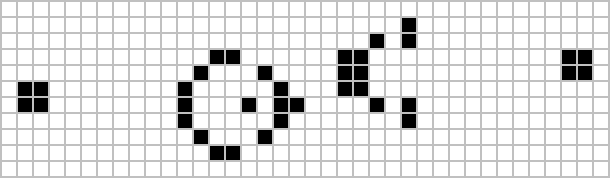 |

ゴスパーのグライダー銃。30世代毎にグライダーを打ち出す。
□□□□□■□□□ □□□□□□■□□ □□■□□□■□□ □□□■■■■□□ □□□□□□□□□ □□□□□□□□□ □□□□□□□□□ □□■□□□□□□ □□□■■□□□□ □□□□■□□□□ □□□□■□□□□ □□□■□□□□□ □□□□□□□□□ □□□□□□□□□ □□□□□■□□□ □□□□□□■□□ □□■□□□■□□ □□□■■■■□□
|
繁殖型の中には時間の2乗に比例した増加を示すパターンがありそれらは「ブリーダー」と呼ばれる。これもゴスパーにより発見された。
繁殖型には後にもっと単純なものが見つかっている。次の3つはいずれも、無限に増え続けるパターンに成長する初期配置である。1つ目のパターンは初期配置ではわずか10個のセルしか生きておらず(これが最少であることが証明されている)、2つ目のパターンは5×5に収まっている。3つ目のパターンはわずか1列である。(いずれも「スイッチ機関車」をベースとしたパターンになる。初期配置は小さいが、成長過程は単純ではない)
 |  |
 | |
成長過程が単純なものとしては、以下のようなシュシュポッポ列車がある。
このパターンは、後方にブリンカーを残してゆく(図では2列が既に現れている)。
長寿型の例
非常に長い間変化を続ける長寿型(メトセラ)と呼ばれるパターンがある。「ダイハード」は130世代後に死滅するパターンであり、「ドングリ」(acorn) は13個のグライダーを生み出すのに5206世代かかるパターンである。
| ダイハード | ドングリ |
|---|---|
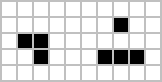 |
バリエーション
オリジナルのライフゲーム以外にも様々な新しいルールを考えることができる。
周囲に3つの隣人がいれば生命が誕生し、周囲に2つか3つの隣人がいれば生き残りそれ以外の場合では死ぬというルールである標準のライフゲームを23/3と表す。最初の数 (2,3) は生き残るために必要な数を表し、次の数 (3) は生命の誕生に必要な数を表す。従って16/6は、「6つの隣人がいればセルが誕生し、1つあるいは6つの隣人がいれば生き残る」ことを意味する。41/2は産まれたらすぐ死ぬ。
バリエーションの中では、23/36が有名である。HighLifeと呼ばれ、オリジナルのルールに加えて、6つの隣人がいれば誕生するというルールを付け加えたものである。
また、一般的なライフゲームでうまくいかない点を研究するために、3-4Lifeなどの変則ルールが多数作られている。
また、「2次元平面とムーア近傍」以外の空間における、類似したルールによるセル・オートマトン、といったものも考えることができる。[2]
ライフゲームを用いた計算機
ライフゲームはチューリング完全であり、チューリングマシンと同等の計算能力を持つ。これは、ライフゲームのパターンで計算機を形成し、その上でプログラムを実行する事が可能である事を示している。
計算機を構成するために必要な要素として、グライダーなどのパターンの組み合わせでAND、OR、NOTなどの論理ゲートを構築できる。グライダーを利用することで他のオブジェクトとの相互作用を得られる。例えばブロックを近くに運んできたり遠くへ移動させたりすることができる。この移動機構はカウンタとして利用できる。
他にも様々な計算能力を持つパターンが発見されている。素数/乱数生成器や、ライフゲームを用いてライフゲームを計算する "Unit cell" などは、実際に動作する計算機としてのライフゲームの例である。
脚注
^ 英語で単に "The Game of Life" とした場合、ハズブロが販売しているボードゲームと同名(日本では「人生ゲーム」)だが、これとは全く無関係である。これと区別するため、ライフゲームを "Conway's Game of Life" 、人生ゲームを "Hasbro's Game of Life" とも呼ぶ。
^ いくつかの例がNAID 40000002718にある。
参考文献
- A・K・デュードニー 『遊びの展開 コンピューターレクリエーション4』 日経サイエンス〈別冊日経サイエンス 113〉、1995年6月。ISBN 4-532-51113-5。
ウィリアム・パウンドストーン 『ライフゲイムの宇宙』 有沢誠訳、日本評論社、1990年6月。ISBN 4-535-78174-5。
- ウィリアム・パウンドストーン 『ライフゲイムの宇宙』 有沢誠訳、日本評論社、2003年6月、新装版。ISBN 4-535-78383-7。
- 上岡義雄 『神になる科学者たち 21世紀科学文明の危機』 日本経済新聞社、1999年12月。ISBN 4-532-14798-0。
- ピーター・W・アトキンス 『エントロピーと秩序 熱力学第二法則への招待』 米沢富美子・森弘之訳、日経サイエンス社、1992年6月。ISBN 4-532-52014-2。
Gardner, Mertin (1970年10月). “Mathematical games”. Scientific American (Nature Publishing Group) 223: pp. 120-123.
Gardner, Mertin (1971年2月). “Mathematical games”. Scientific American (Nature Publishing Group) 224: pp. 112-117.
関連項目
- 人工生命
- セル・オートマトン
- カオス理論
- エデンの園配置
- ライフゲームの物体一覧
- ハッシュライフ
外部リンク
LifeWiki - ライフゲームに関するウィキサイト
http://www.conwaylife.com/wiki/Conway's_Game_of_Life LifeWikiのConway's Game of Lifeの記事
Life Lexicon(英語)
http://www.bitstorm.org/gameoflife/lexicon/#pl Life LexiconのLifeの項目
Conway's Game of Life as an Java Applet(※リンク切れ?)- Eric Weisstein's Treasure Trove of the Life C.A.(英語)
- Vector: ライフゲーム(Windows上で動作するライフゲームのプログラムがある)
- Golly(オープンソースのライフゲームシミュレータ、例が豊富)
- ライフゲーム入門 for Mac OS X
- ライフゲーム(Java)
- 2次元のセル・オートマトン(Java)
- コンウェイのライフゲーム Java および HTML5 における実装の例。
| ||||||||||||||||